算法课第二次作业

一、Money robbing

1、optimal substructure and DP equation

对于第 i 家，有两种选择，抢或者不抢。如果抢第 i 家，那么最大收益为：value[i] + 抢前 i-2 家的最优收益；如果第 i 家不抢，那么最大收益为：抢前 i-1 家的最优收益。

状态转移方程可写为：
$$
dp[i] = max( dp[i-1], dp[i-2]+value[i] )
$$

2、 pseudo-code

class Solution {
public:
    int rob(vector<int>& nums){
        if( nums.size()==0 )
            return 0;
        else if( nums.size()==1 )
            return nums[0];
        vector<int> dp(nums.size(),0);
        dp[0] = nums[0];
        dp[1] = max( nums[0], nums[1] );
        for( int i=2; i<nums.size(); i++ ){
            dp[i] = max( dp[i-1], dp[i-2]+nums[i] );
        }
        return dp[nums.size()-1];
    }
};

3、 correctness of algorithm

如果暴力求解的话，每一家都有可能抢或者不抢，枚举每一种可能性，那么总的时间复杂度为 $O(2^n)$ ，且最后算出来的最优解一定是正确的。现在，我们采用动态规划思想中的 memory 数组，记录前 i-1 家的最优值，当计算第 i 家最优值时，其依赖的 OPT[i-1] 和 OPT[i-2] 已经求出，可直接计算当前最优值，故算法是正确的。

4、 complexity of algorithm

代码中的 dp 数组，每个元素只计算了一遍，故算法的时间复杂度为 $ O(n) $。

注：

当房屋变成一个环的时候，也就是相当于在原有问题上添加了一个限制条件：第1家和第n家不能同时抢。那么，分别计算抢第二家到最后一家与抢第一家到倒数第二家的最大值，取两个值中更大的那个就是结果。

LeetCode 213题

class Solution {
public:
    int rob(vector<int>& nums) {
        if( nums.size()==0 )
            return 0;
        else if( nums.size()==1 )
            return nums[0];
        return max( func(nums, 0), func(nums, nums.size()-1 ));
    }
    int func( vector<int> nums, int pos ){
        nums.erase(nums.begin()+pos);
        if( nums.size()==0 )
            return 0;
        else if( nums.size()==1 )
            return nums[0];
        vector<int> dp(nums.size(),0);
        dp[0] = nums[0];
        dp[1] = max( nums[0], nums[1] );
        for( int i=2; i<nums.size(); i++ ){
            dp[i] = max( dp[i-1], dp[i-2]+nums[i] );
        }
        return dp[nums.size()-1];
    }
};

二、Node selection

1、optimal substructure and DP equation

对于当前根节点，有两种可能性，选取或者不选取。如果选取了当前的根节点，那么其孩子节点就不能选取，即最优值变为：root->value + 4个孙子的最优值之和；如果当前根节点没有选取，最优值变为：两个孩子节点最优值之和。

给定任意一个根，假设我们能够得到当前根选取与不选取的最优值，结果保存在一个长度为2的数组里，array[0]代表根节点不选取，array[1]代表根节点选取，那么最优解为：

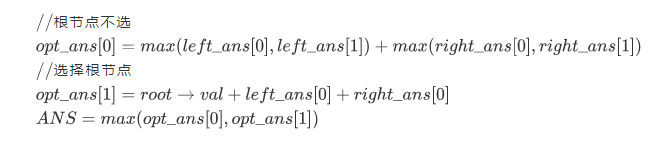
2、 pseudo-code

LeetCode 337题

class Solution {
public:
    int rob(TreeNode* root) {
        vector<int> ans = solve( root );
        return max( ans[0], ans[1] );
    }
    vector<int> solve( TreeNode* root ){
        vector<int> ans(2,0);
        if( !root )
            return ans;
        vector<int> left_ans = solve( root->left);
        vector<int> right_ans = solve( root->right );
        ans[0] = max( left_ans[0], left_ans[1] ) + max( right_ans[0], right_ans[1] ); //根节点不选
        ans[1] = root->val + left_ans[0] + right_ans[0]; //选择根节点
        return ans;
    }
};

3、correctness of algorithm

当前节点的最优值，依赖于其儿子节点的最优值（当前节点没选，最优值等于选其左孩子节点最优值+选其右孩子节点最优值）或其孙子节点的最优值（选取了当前节点，最优值等于根节点值+其左孩子不选左根的最优值+右孩子不选右根的最优值），由此可知算法的正确性。

4、complexity of algorithm

整个算法相当于一个深度优先搜索（DFS），树中的每个节点都会遍历一次，故算法的时间复杂度为$O(n)$。

三、Decoding

1、optimal substructure and DP equation

dp[i]表示从字符0~i的字符串包含最多的编码种数。不考虑特殊情况，该题的递推式是$dp[i]=dp[i-1]+dp[i-2]$，因为一个数字可以表示一个编码，两个数字也有可能表示一个编码，所以dp[i]应该等于0~i-1的字符串包含的最多编码种数加上0~i-2的字符串包含的最多编码种数。但是考虑到一共只有26种基础编码加上特殊情况0，所以递推式可以表示为：

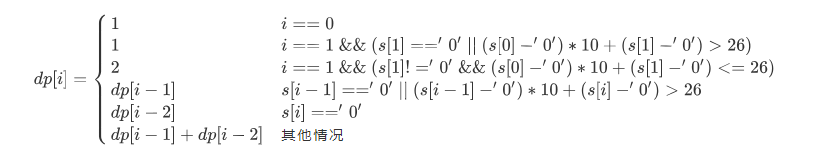
2、 pseudo-code

LeetCode 91题

class Solution {
public:
    int numDecodings(string s) {
        if( s.length()==0 || s[0]=='0' ) return 0;
        vector<int> dp(s.length()+1,0);
        dp[0] = dp[1] = 1;
        for( int i=1; i<s.length(); i++ ){
            if( s[i]!='0' )
                dp[i+1] += dp[i];
            if( s[i-1]!='0' && (s[i-1]-'0')*10+(s[i]-'0')<=26 )
                dp[i+1] += dp[i-1];
        }
        return dp[s.length()];
    }
};

3、correctness of algorithm

首先该问题包含最优子结构的性质，求0~n的字符串包含最多的编码种数包含了求0~n-1的字符串包含最多的编码种数或0~n-2的字符串包含最多的编码种数。其次该问题包含重叠子性质，大量子问题会重复计算，如求dp[5]需要计算dp[4]或dp[3],求dp[4]需要求dp[3]或dp[2]，因此dp[3]被重复计算。综上该问题可以用动态规划方法解且求解方程正确。

4、complexity of algorithm

整个求解过程只遍历了一遍字符串，故算法时间复杂度为$O(n)$。

六、OJ第一题

LIS，DP入门第一题，没啥好说的，只要想清楚为啥每次将新来的数据往 ans 数组里插入，最后出来的就一定是最长的就可以了。

#include <bits/stdc++.h>

using namespace std;

int main(){
    int num, T, N;
    int length, index;
    int ans[100005];
    cin >> T;
    for( int t = 0; t<T; t++ ){
        cin >> N;
        length = 0;
        memset(ans, -1, sizeof(ans));
        for( int i=0; i<N; i++ ){
            scanf("%d",&num);
            index = lower_bound( ans, ans+length, num ) - ans;
            ans[index] = num;
            if( index==length )
                length++;
        }
        cout << length << endl;
    }
    return 0;
}

七、OJ第二题

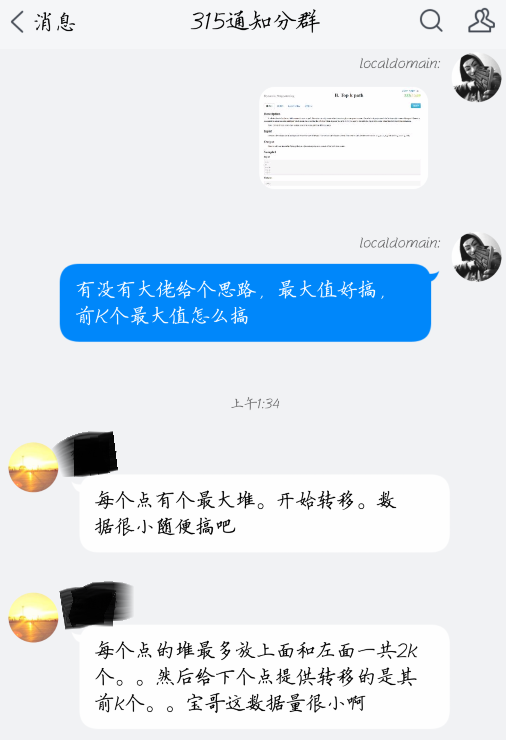
入门级题目外加了求 K 个最优值的条件，昨晚1点多打开题目，感觉随便码一码随便A掉，于是上床睡觉，躺床上拍脑袋理论AC。仔细一想，K个最优值的状态转移，有点问题啊，带着疑问入睡不咋舒坦，大半夜将题目发到315群，杨老师帅气得给出了解决方案，顺带嘲笑了一波数据；炸老师看了数据量也嘲讽了一波；早上起来交了一发，发现 0 ms的时候，也疯狂鄙视一波，数据真的弱得不行。

想起来当年 ycb 的誓言：

#include <bits/stdc++.h>

using namespace std;

int m, n, k;
int num;
priority_queue<int> ans[105], cur_ans, tmp_ans;//默认大堆

int main(){
    ans[1].push(0);
    cin >> m >> n >> k;
    for( int i=1; i<=m; i++ ){
        for( int j=1; j<=n; j++ ){
            scanf("%d", &num);
            while( !cur_ans.empty() ){  //清空cur_ans
                cur_ans.pop();
            }
            tmp_ans = ans[j-1];
            while( !ans[j-1].empty() ){
                cur_ans.push(ans[j-1].top()+num);
                ans[j-1].pop();
            }
            ans[j-1] = tmp_ans;
            while( !ans[j].empty() ){
                cur_ans.push(ans[j].top()+num);
                ans[j].pop();
            }
            while( ans[j].size()<k && !cur_ans.empty() ){
                ans[j].push(cur_ans.top());
                cur_ans.pop();
            }
        }
    }
    cout << ans[n].top();
    ans[n].pop();
    while( !ans[n].empty() ){
        cout << " " << ans[n].top();
        ans[n].pop();
    }
    return 0;
}