算法课第一次作业

发表于 | 更新于: | 分类于 ， | | 阅读次数:
字数统计: 3.4k 字 | 阅读时长 ≈ 16 分钟

一、Divide and Conquer

　　You are interested in analyzing some hard-to-obtain data from two separate databases. Each database contains n numerical values, so there are 2n values total and you may assume that no two values are the same. You’d like to determine the median of this set of 2n values, which we will define here to be the n-th　smallest value.

　　However, the only way you can access these values is through queries to the databases. In a single query, you can specify a value k to one of the two databases, and the chosen database will return the kth smallest value that it contains. Since queries are expensive, you would like to compute the median using as few queries as possible.

Give an algorithm that finds the median value using at most O(logn) queries.　　

1、problem-solving ideas and pseudo-code

首先将现实问题转化一下，变成计算机算法问题，即 找2个有序数组的并集的中位数 ，LeetCode 第四题。

(1）problem-solving ideas

求中位数需要根据数组长度是奇数还是偶数分别讨论，奇数长度时中位数为最中间的一个数，偶数长度时中位数为最中间的两个数的平均值，为了方便，可以实现一个比题目更一般化的函数，求A和B的第k小数的函数，那么中位数的问题很容易解决。

求一个有序数组的第k个数只需要O(1)的复杂度，现在有两个数组，显然花费额外空间以O(n)时间归并然后O(1)寻找不满足题目要求。既然要求log时间复杂度，一般需要使用到二分思想。

分别考虑A和B的第k/2个元素：

  • 如果它们相等，则第k个数为其中的任意一个
  • 如果A中的比较大，则B中前k/2个元素都不可能是第k个数了，因为这个数至少应该为A的第k/2个数，把B的前k/2去掉，然后重新寻找。
  • 如果B中的比较大，则把A的前k/2个数去掉，重新寻找。

直到A和B中某个变为空时或者寻找第1个数时可以停止递归，直接找到结果。

注意，上面的k/2只是理想的简单情况，实际上A和B的长度可能不够k/2，或者k为奇数等，但这些不是主要问题，可以让A取第k/2个数字，然后A不够长，则取A的最后一个数字，然后B取剩下长度对应的那个数字，具体参考代码。

(2）pseudo code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int totalLength = nums1.size() + nums2.size();
    if( totalLength&1 )
        return findKth( nums1.begin(), nums1.size(), nums2.begin(), nums2.size(), (totalLength>>1)+1 );
    else //除以 2.0 是为了保留小数点
        return (findKth( nums1.begin(), nums1.size(), nums2.begin(), nums2.size(), (totalLength>>1) ) + findKth( nums1.begin(), nums1.size(), nums2.begin(), nums2.size(), (totalLength>>1)+1 ))/2.0;
}
int findKth( vector<int>:: iterator nums1, int len1, vector<int>:: iterator nums2, int len2, int k ){
	// 默认 len1 要大于 len2
    if( len1<len2 )
        return findKth( nums2, len2, nums1, len1, k );
    if( len2==0 )
        return nums1[k-1];
    if( k==1 )  //k==1做特判，因为后期要移位, 不做特判point-1会出现负值
        return min( nums1[0], nums2[0] );
    int point2 = min( k>>1, len2 );
    int point1 = k - point2;
    //下面对 nums1[point1-1] 和 nums2[point2-1]的大小关系进行讨论
    if( nums1[point1-1] > nums2[point2-1] )
        return findKth( nums1, point1, nums2+point2, len2-point2, k-point2 );
    else if( nums1[point1-1] < nums2[point2-1] )
        return findKth( nums1+point1, len1-point1, nums2, point2, k-point1 );
    else
        return nums1[point1-1];
    }

2、subproblem reduction graph

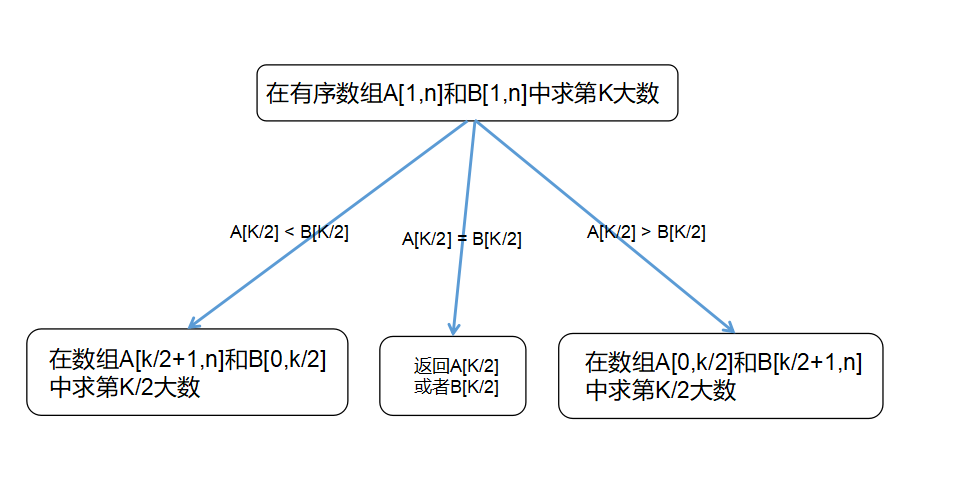
问题缩减图

3、prove the correctness

寻找两个有序数组的第K大数，那么肯定是第1个数组贡献 a 个数，第二个数组贡献 K - a 个数。首先我们假设每个数组分别贡献 K/2个数，讨论 A[k/2] 和 B[k/2] 的大小情况。

当 A[k/2] > B[K/2] 时，很显然需要减少数组A贡献的数字的个数，增加数组B贡献的数组的个数，如下图：

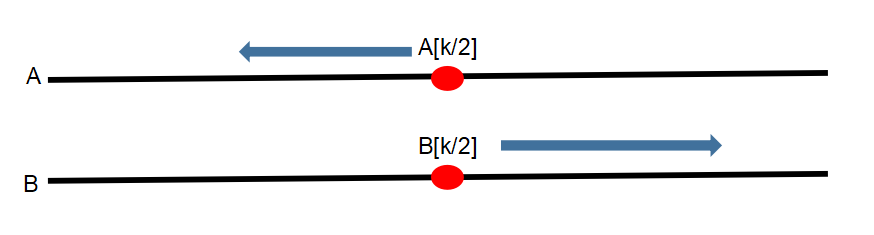
当 A[k/2] < B[K/2] 时，很显然需要增加数组A贡献的数字的个数，减少数组B贡献的数组的个数，如下图：

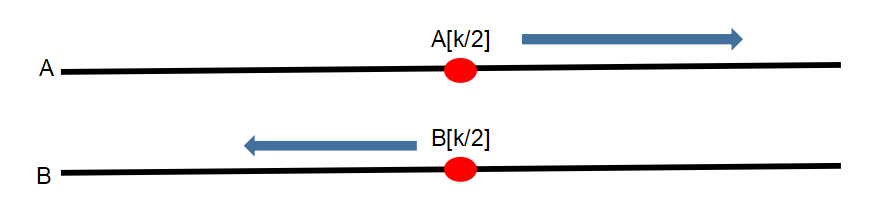
随着算法的执行，搜索的数组长度不断缩小，最后一定会返回对应的中位数值。

4、the complexity of this algorithm

分析可得：

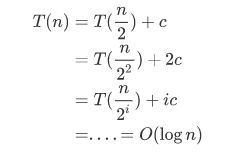
五、Divide and Conquer

　　Recall the problem of finding the number of inversions. As in the course, we are given a sequence of n numbers a1,··· ,an, which we assume are all distinct, and we define an inversion to be a pair i < j such that ai > aj.

　　We motivated the problem of counting inversions as a good measure of how different two orderings are. However, one might feel that this measure is too sensitive. Let’s call a pair a significant inversion if i < j and ai > 3aj. Given an O(nlogn) algorithm to count the number of significant inversions between two orderings.

1、problem-solving ideas and pseudo-code

(1）problem-solving ideas

求数列的逆序数，除了暴力求解方式外，也可以使用归并排序、树状数组、线段树等结构进行计算。此处选择使用归并排序。

首先，将数组从中间切开，分为左右两半，A[0…n/2] 和 A [n/2+1…n]，分别计算这两个子问题的显著逆序数；

然后，计算跨左右两边的数对所形成的显著逆序的个数。

最后，将这三者的显著逆序数求和，即为整个数组的显著逆序数。

(2）pseudo code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
//统计变量num为全局变量
void mergesort(int begin, int end){
	if (begin >= end)
		return;
	int mid = (begin + end) / 2;
	mergesort(begin, mid);
	mergesort(mid + 1, end);
	mcount(begin, mid, end);
	merge(begin, mid, end);
}

void mcount(int begin, int mid, int end){
	int i = begin;
	int j = mid + 1;
	int k = begin;
	while (i <= mid && j <= end){
		if (a[i] > 2 * a[j]){
			num += mid - i + 1;
			j++;
		}
		else
			i++;
	}
}
 
void merge(int begin, int mid, int end){
	int i = begin;
	int j = mid + 1;
	int k = begin;
 
	while (i <= mid && j <= end){
		if (a[i] > a[j]){
			temp[k] = a[j];
			k++;
			j++;
		}
		else{
			temp[k] = a[i];
			k++;
			i++;
		}
	}
	while (i <= mid){
		temp[k] = a[i];
		k++;
		i++;
	}
	while (j <= end){
		temp[k] = a[j];
		k++;
		j++;
	}
	for (int p = begin; p <= end; p++)
		a[p] = temp[p];
}

2、subproblem reduction graph

先分：

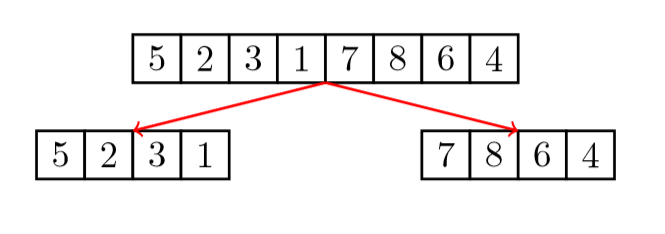
后合：

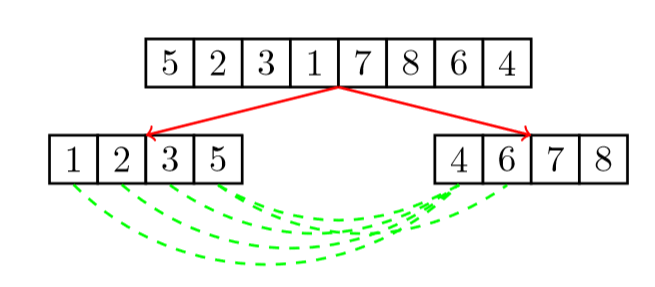
3、prove the correctness

其中，计算左右两边的显著逆序数的时候，会同时将左右两边的子数组变成有序。在计算跨两边的数对所形成的显著逆序的时候，就不用进行暴力遍历，只需O(n)的遍历即可。当 L[i] > 3*R[j] 时，RC += |L|-i 即可，L中位于下标 i 之后的数字就不用遍历了，自然要比 3*R[j] 大。
同时，计算过程是基于归并排序的，整个算法即正确。

4、the complexity of this algorithm

计算左边的时间复杂度为 T(n/2)， 计算右边的时间复杂度为 T(n/2)， 合并的时间复杂度为 O(n)，所以总的时间复杂度为：

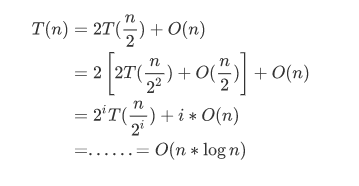
六、Divide and Conquer

Given a table M consisting of 2n ∗ 2n blocks, we want to fill it with a L-shaped module (consisting of three blocks). The L-shaped module is shown below.

Please give a fill method, so that the last element of the table (M2n,2n) is empty.

For example:

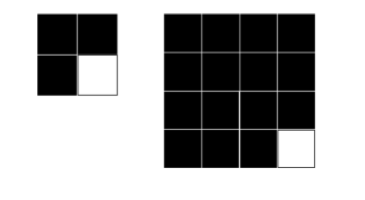
1、problem-solving ideas and pseudo-code

(1）problem-solving ideas

　　有一个特殊方格的棋盘覆盖问题，只不过，此题目将特殊方格定死了，只能为最右下角那个，即 P(size-1,size-1)那个小方格。

　　该题关键在于如何划分各L型骨牌所在位置区域。我们发现，L型骨牌占三个方格，我们可以把棋盘从中央分为四块，那么这四块子棋盘中仅一块是有特殊方格的，可以用一块骨牌使得其他三块子棋盘均被覆盖。以此为原则，无论这种分法是否最终可解，我们首先保证了每个子棋盘都有一个特殊方格，所以，分治的模型就出来了。

　　我们可以用递归来完成分治的任务。每次递归，chess_board(int posx,int posy,int x,int y,int size)，(posx,posy)为子棋盘左上角坐标,size为子棋盘大小，因为棋盘总为正方形，所以size为边长，那么这3个参数就确定了子棋盘的位置和大小；(x,y)表示子棋盘中特殊方格的位置，这个位置是由上层递归分配骨牌后决定的。以此为标准，递归流程为：

①判断边界，若当前棋盘大小为1，则无法再分割，递归结束。

②定子棋盘中心位置。

③判断特殊方格所在位置（左上，右上，左下，或右下）。

④根据特殊方格位置确定所选L型骨牌，原特殊方格和三个L型骨牌的方格分别为四个子棋盘的特殊方格。

⑤依据④中判断，按编号填充棋盘。

⑥4次递归，分别对应四个子棋盘。

(2）pseudo code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
void chess_board(int posx,int posy,int x,int y,int size){
	if( size==1 )
		return ;
	size /= 2;
	int num = Count++;
	//左上角
	if( posx+size>x && posy+size>y )
		chess_board(posx,posy,x,y,size);
	else{
		board[posx+size-1][posy+size-1] = num;
		chess_board(posx,posy,posx+size-1,posy+size-1,size);
	}

	//右上角
	if( y>=posy+size && x<posx+size )
		chess_board(posx,posy+size,x,y,size);
	else{
		board[posx+size-1][posy+size] = num;
		chess_board(posx,posy+size,posx+size-1,posy+size,size);
	} 
	
	//左下角
	if( x>=posx+size && y<posy+size )
		chess_board(posx+size,posy,x,y,size);
	else{
		board[posx+size][posy+size-1] = num;
		chess_board(posx+size,posy,posx+size,posy+size-1,size);
	} 
	
	//右下角
	if( x>=posx+size && y>=posy+size )
		chess_board(posx+size,posy+size,x,y,size);
	else{
		board[posx+size][posy+size] = num;
		chess_board(posx+size,posy+size,posx+size,posy+size,size);
	}
}

2、subproblem reduction graph

假设有如下图的一个棋盘，棋盘中有一个特殊方格：

第一次分割：

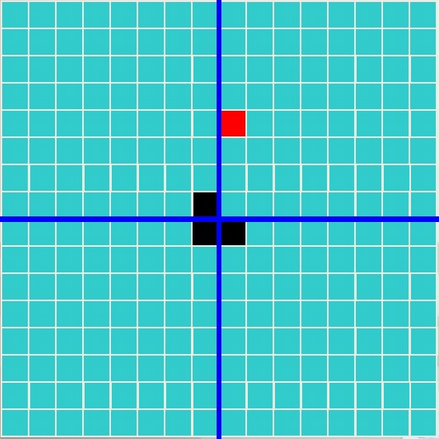
第二次分割：

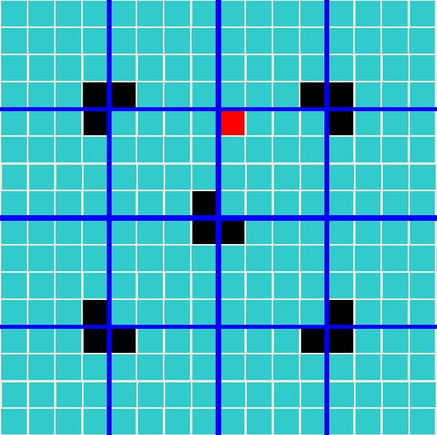
第三次分割：

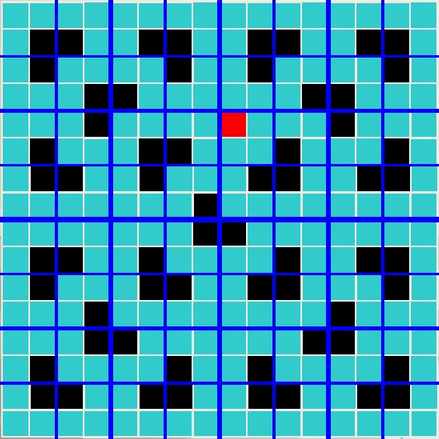
第四次分割：

最后解的形式如下图所示（右下角空）：

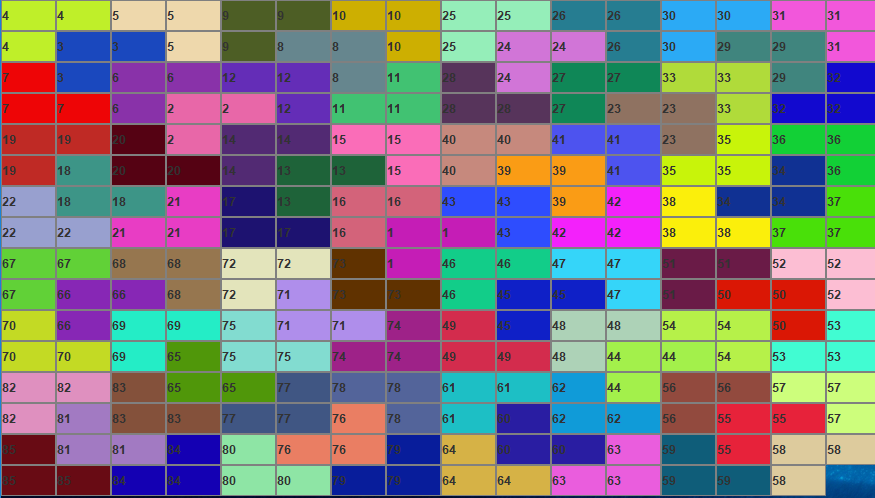
3、prove the correctness

使用数学归纳法：

（1）k = 1 时, 有解

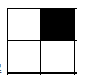
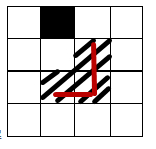
（2）k = 2 时，有解：

（3）设 k-1 时成立(k>2)，将 2^k 2^k 棋盘分割为 4 个 2^(k-1) 2^(k-1) 子棋盘，如下图所示：

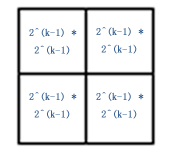
特殊方格必位于 4 个较小子棋盘之一中，其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊盘，我们可以用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处，如下图所示，这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格，从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用这种分割，直至棋盘简化为 2^1x2^1 棋盘。

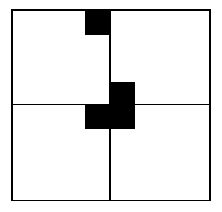
综上可得，该算法正确，最终可求得想要的结果。

4、the complexity of this algorithm

算法的时间复杂度递推式如下：

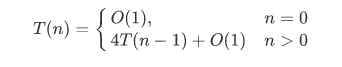
即：

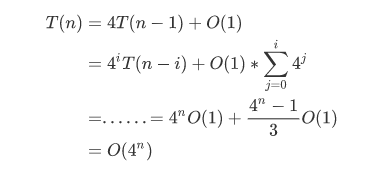
七、OJ第一题（寻找第K大数）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>

using namespace std;

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        vector<int> small, big;
        srand(time(NULL));
        int pivotIndex = rand()%nums.size();
        for( int i=0; i<nums.size(); i++ ){
            if( i==pivotIndex )
                continue;
            if( nums[i]>nums[pivotIndex] )
                big.push_back(nums[i]);
            else
                small.push_back(nums[i]);
        }
        if( big.size() == k-1 )
            return nums[pivotIndex];
        else if( big.size() > k-1 )
            return findKthLargest( big, k );
        else
            return findKthLargest( small, k-big.size()-1 );
    }
};

int main(){
    int n, k;
    cin >> n >> k;
    vector<int> vec;
    int num;
    for( int i=0; i<n; i++ ){
        scanf("%d", &num);
        vec.push_back(num);
    }
    Solution s;
    cout << s.findKthLargest(vec,k) << endl;
    return 0;
}

八、OJ第二题（二维最近点对）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include <bits/stdc++.h>

using namespace std;

vector< pair<double, double> > point;

double calcDist( pair<double, double> p1, pair<double, double> p2 ){
    return (p1.first-p2.first)*(p1.first-p2.first) + (p1.second-p2.second)*(p1.second-p2.second);
}

bool compare_x( pair<double, double> p1, pair<double,double> p2 ){
    return p1.first<p2.first;
}
bool compare_y( pair<double, double> p1, pair<double,double> p2 ){
    return p1.second<p2.second;
}

pair< pair<double, double>, pair<double, double> > solution( vector< pair<double, double> >& vec ){
    if( vec.size()<=3 ){ //当点的个数小于3个时，直接暴力求解,想一下为啥是3
        pair< pair<double, double>, pair<double, double> > ans = make_pair(vec[0], vec[1]);
        if( vec.size()==3 ){
            double dst01 = calcDist( vec[0], vec[1] );
            double dst12 = calcDist( vec[1], vec[2] );
            if( dst01>dst12 )
                ans = make_pair(vec[1], vec[2]);
            double dst02 = calcDist( vec[0], vec[2] );
            if( calcDist(ans.first, ans.second)>dst02 )
                ans = make_pair(vec[0], vec[2]);
        }
        return ans;
    }

    //分开,左右两部分
    sort( vec.begin(), vec.end(), compare_x );  //并不是使用pivot，直接分一半过去
    vector< pair<double, double> > pointLeft( vec.size()/2 );
    copy( vec.begin(), vec.begin()+vec.size()/2, pointLeft.begin() );
    vector< pair<double, double> > pointRight( vec.size() - vec.size()/2 );
    copy( vec.begin()+vec.size()/2, vec.end(), pointRight.begin() );
  
    pair< pair<double, double>, pair<double, double> > ansLeft = solution( pointLeft );
    pair< pair<double, double>, pair<double, double> > ansRight = solution( pointRight );

    double dst = calcDist(ansLeft.first, ansLeft.second);
    pair< pair<double, double>, pair<double, double> > ans = ansLeft;
    if( calcDist(ansLeft.first, ansLeft.second) > calcDist(ansRight.first, ansRight.second) ){
        ans = ansRight;
        dst = calcDist(ansRight.first, ansRight.second);
    }
    //计算中间
    double pivot = ( pointLeft[pointLeft.size()-1].first + pointRight[0].first ) / 2.0;
    vector< pair<double, double> > pointMiddle;
    for( int i=0; i<vec.size(); i++ ){
        if( (pivot-vec[i].first)*(pivot-vec[i].first) < dst )
            pointMiddle.push_back( vec[i] );
    }
    sort( pointMiddle.begin(), pointMiddle.end(), compare_y );
    for( int i=0; i<pointMiddle.size(); i++ ){
        for( int j=1; j<=7 && (i+j)<pointMiddle.size(); j++ ){
            if( calcDist( pointMiddle[i], pointMiddle[i+j] ) < dst ){
                dst = calcDist( pointMiddle[i], pointMiddle[i+j] );
                ans = make_pair( pointMiddle[i], pointMiddle[i+j] );
            }
        }
    }
    return ans;
}

int main(){
    int n;
    double x, y;
    cin >> n;
    for( int i=0; i<n; i++ ){
        scanf("%lf %lf", &x, &y);
        point.push_back( make_pair(x,y) );
    }
    pair< pair<double, double>, pair<double, double> > ans;
    ans = solution(point);
    double mindst = calcDist( ans.first, ans.second );
    printf("%.2f\n", sqrt(1.0*mindst));
    //cout << "(" << ans.first.first << "," << ans.first.second << ")" << ",  (" << ans.second.first << "," << ans.second.second << ")" << endl;
    return 0;
}
-------------本文结束感谢您的阅读-------------
您的鼓励就是我创作的动力，求打赏买面包~~
0%