LeetCode1-10

1、两数之和

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> Map;
        vector<int> ans;
        for(int i=0; i<nums.size(); i++)
            Map[nums[i]] = i;
        for(int i=0; i<nums.size(); i++){
            int tmp = target - nums[i];
            if( Map.count(tmp) && Map[tmp]!=i ){
                ans.push_back(i);
                ans.push_back(Map[tmp]);
                break;
            }
        }
        return ans;
    }
};

2、两数相加

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode* res = new ListNode(0);
        ListNode* tmp = res;
        int sum = 0;
        while( l1 || l2 ){
            if( l1 ){
                sum += l1->val;
                l1 = l1->next;
            }
            if( l2 ){
                sum += l2->val;
                l2 = l2->next;
            }
            tmp->next = new ListNode(sum%10);
            tmp = tmp->next;
            sum /= 10;
        }
        if( sum )
            tmp->next = new ListNode(sum);
        return res->next;  //解决的很是巧妙
    }
};

3、无重复字符的最长子串

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        int ans = 0;
        int i, j;
        map<char, int> mp;
        for( i=0,j=0; j<s.length(); j++ ){
            if( mp.count(s[j]) == 0 ){  //map中之前不含有此元素
                mp.insert(make_pair( s[j], j ));
            }
            else{  //map中之前含有此元素
                ans = max( ans, j-i );
                i = max( mp[s[j]]+1, i );
                mp[s[j]] = j;
            }
        }
        ans = max( ans, j-i ); //到字符串的结尾了，需要处理
        return ans;
    }
};

4、两个排序数组的中位数

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int totalLength = nums1.size() + nums2.size();
        if( totalLength&1 )
            return findKth( nums1.begin(), nums1.size(), nums2.begin(), nums2.size(), (totalLength>>1)+1 );
        else //除以 2.0 是为了保留小数点
            return (findKth( nums1.begin(), nums1.size(), nums2.begin(), nums2.size(), (totalLength>>1) ) + findKth( nums1.begin(), nums1.size(), nums2.begin(), nums2.size(), (totalLength>>1)+1 ))/2.0;
    }
    int findKth( vector<int>:: iterator nums1, int len1, vector<int>:: iterator nums2, int len2, int k ){
        // 默认 len1 要大于 len2
        if( len1<len2 )
            return findKth( nums2, len2, nums1, len1, k );
        if( len2==0 )
            return nums1[k-1];
        if( k==1 )  //k==1做特判，因为后期要移位, 不做特判point-1会出现负值
            return min( nums1[0], nums2[0] );
        int point2 = min( k>>1, len2 );
        int point1 = k - point2;
        //下面对 nums1[point1-1] 和 nums2[point2-1]的大小关系进行讨论
        if( nums1[point1-1] > nums2[point2-1] )
            return findKth( nums1, point1, nums2+point2, len2-point2, k-point2 );
        else if( nums1[point1-1] < nums2[point2-1] )
            return findKth( nums1+point1, len1-point1, nums2, point2, k-point1 );
        else
            return nums1[point1-1];
    }
};

5、最长回文子串

Manacher算法，国内也叫“马拉车”。虽然 RL[i]=min(RL[2*pos-i], MaxRight-i)，但是位于 i 半径右边界与 MaxRight之间的元素是不会被重复遍历的，否则会与 i 的对称 j 起冲突，也正因为如此，算法的复杂度是 O(n)。

class Solution {
public:
    string longestPalindrome(string s) {
        string newString = "#";
        for( int i=0; i<s.length(); i++ ){
            newString += s[i];
            newString += "#";
        }
        int maxLen = 0, maxLenIndex = 0;
        int maxRight=0, pos=0; //代表当前最右及其对应中心元的位置
        int radius[newString.length()];
        for( int i=0; i<newString.length(); i++ ){
            if( i<maxRight )
                radius[i] = min( radius[2*pos-i], maxRight-i+1 ); //注意这里的 +1
            else
                radius[i] = 1;
            while( (i+radius[i])<newString.length() && (i-radius[i])>=0 && newString[i+radius[i]]==newString[i-radius[i]] ){ // i+radius[i]-1为当前所到位置
                radius[i] += 1;
            }
            //更新 maxRight 和 pos
            if( (i+radius[i]-1)>maxRight ){
                maxRight = i+radius[i]-1;
                pos = i;
            }
            if( maxLen<radius[i] ){
                maxLen = radius[i];
                maxLenIndex = i;
            }
        }
        string ansString = "";
        for( int i=maxLenIndex-radius[maxLenIndex]+1; i<maxLenIndex+radius[maxLenIndex]-1; i++ ){
            if( newString[i]!='#' )
                ansString += newString[i];
        }
        return ansString;
    }
};

6、Z字形变换

规律题，多些几个即可找到下标间的规律。

class Solution {
public:
    string convert(string s, int numRows) {
        if( numRows==1 )
            return s;
        string ans = "";
        int total = 2*numRows - 2;
        int curNum, pos;
        pos = 0;
        do{
            ans += s[pos];
            pos += total;
        }while( pos<s.length() );
        for( int i=1; i<numRows-1; i++ ){
            curNum = total - 2*i;
            pos = i;
            do{
                ans += s[pos];
                pos += curNum;
                curNum = total - curNum;
            }while( pos<s.length() );
        }
        pos = numRows - 1;
        do{
            ans += s[pos];
            pos += total;
        }while( pos<s.length() );
        return ans;
    }
};

7、反转整数

class Solution {
public:
    int reverse(int x) {
        long long int num = 0;
        int flag = x<0? -1:1;
        x = abs(x);
        do{
            num = 10*num + x%10;
            x /= 10;
        }while(x);
        num = num*flag;
        if( num>INT_MAX || num<INT_MIN )
            num = 0;
        return int(num);
    }
};

8、字符串转整数 (atoi)

一个简单的模拟题，但不得不说leetcode的测试用例真的是强，考虑了 -1 ，给我报 +1的错，两者都考虑了，报了 -+1 的错，真的每一个可能但错误的细节都考虑到了，强！

class Solution {
public:
    int myAtoi(string str) {
        //先将开始的空余字符去掉
        for( int index=0; index<str.length(); index++ ){
            if( str[index]!=' ' ){
                str = str.substr(index);
                break;
            }
        }
        int flag = 1;
        if( str[0]=='-' ){
            flag = -1;
            str = str.substr(1);
        }
        else if( str[0]=='+' ){
            flag = 1;
            str = str.substr(1);
        }
        long long num = 0;
        for( int i=0; i<str.length(); i++ ){
            if( str[i]>='0' && str[i]<='9' ){
                num = num*10 + (str[i]-'0');
                if( flag*num < INT_MIN )
                    return INT_MIN;
                else if( flag*num > INT_MAX )
                    return INT_MAX;
            }
            else
                break;
        }
        return flag*num;
    }
};

9、回文数

将数字倒过来，比较前后两个数是否相同即可。

class Solution {
public:
    bool isPalindrome(int x) {
        if( x<0 )  return false;
        int y = 0, tmp_x = x;
        while( tmp_x ){
            y = 10*y+(tmp_x%10);
            tmp_x /= 10;
        }
        return x==y;
    }
};

10、正则表达式匹配

动态规划的思想来解决这道题目，对于动态规划类的题目，是比较难的，难在状态转移方程写不出来。

首先，dp[i][j]表示 s 中前 i 个字符和 p 中的前 j 个字符是否匹配。下面对 p 中的第 j 个字符是否是 * 号进行分类讨论（至于为啥是以*号为关键字符进行讨论，自己想想，脑补脑补）。

1、 p[j-1] != '*'：

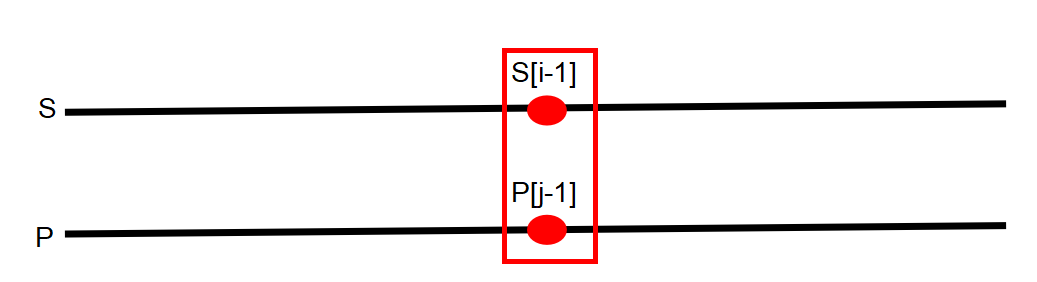
只需要比较 s[i-1] 和 p[j-1] 是否匹配即可，匹配的条件为 s[i-1]==p[j-1] || p[j-1]=='.'，转移方程为：

　　dp[i][j] = dp[i-1][j-1] && (s[i-1]==p[j-1] || p[j-1]=='.')

2、p[j-1] == '*'，分3类情况讨论：

• p[j-1] 的 * 号不起作用，也就是没匹配，此情况下 p[j-2] 和 p[j-1]是作废的，转移方程:

  dp[i][j] = dp[i][j-2]

• p[j-1] 的 * 号匹配一个字符，也就是 P 中的 p[j-2] 和 p[j-1] 所组成的元素和 S 中的 s[i-1]相匹配，所以状态转移方程为：

  dp[i][j] = dp[i-1][j-2] && (s[i-1]==p[j-2] || p[j-2]=='.')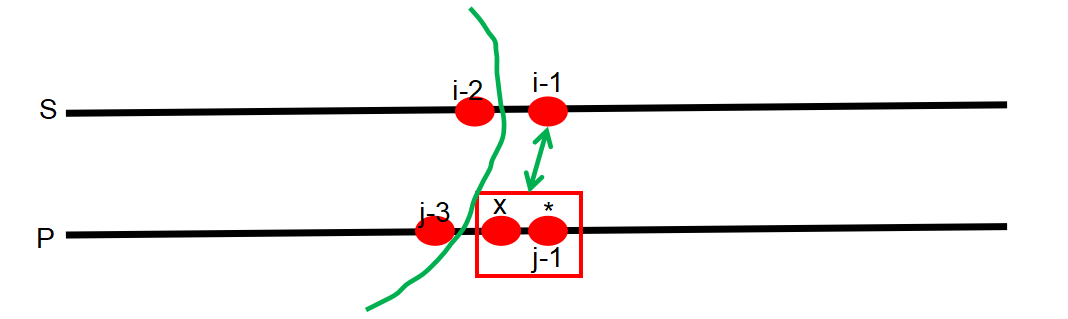

  

• p[j-1] 的 * 号匹配多个字符(>=2)，如下图所示，很容易写出状态转移方程为：

  dp[i][j] =dp[i-1][j] && (s[i-1]==p[j-2] || p[j-2]=='.')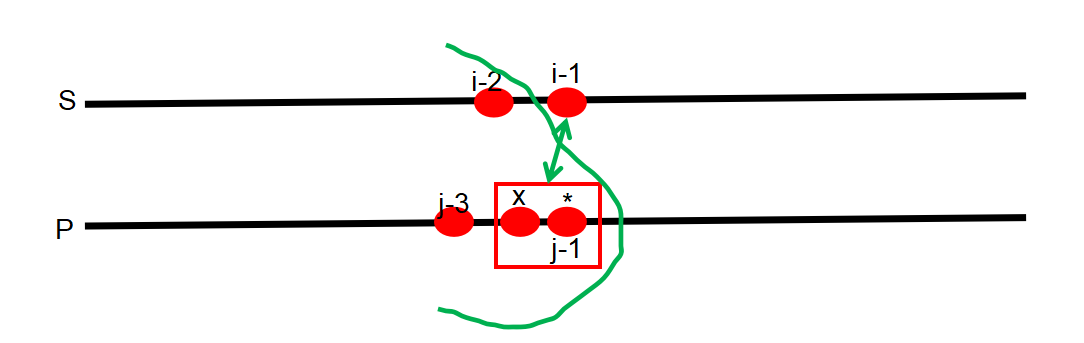

  

  综上所述，总状态转移方程为：

  

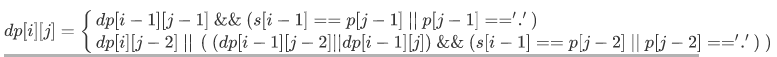
接下来，对初始状态进行讨论：

• 当 S 不空， P 为空时，dp[i][0] = false

• 当 S 空， P 不空时：

  j%2!=0 时，dp[0][j] = false

  j%2==0 时， dp[0][j] = dp[0][j-2] && p[j-1]=='*'

有了以上的分析，代码基本也就写完了，如下：

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.length(), n = p.length();
        bool dp[m+1][n+1];
        dp[0][0] = true;  //都为空，肯定匹配
        // P为空
        for( int i=1; i<=m; i++ )
            dp[i][0] = false;
        // S为空
        for( int j=1; j<=n; j++ ){
            if( j%2==0 )
                dp[0][j] = ( dp[0][j-2] && (p[j-1]=='*') );
            else
                dp[0][j] = false;
        }
        for( int i=1; i<=m; i++ ){
            for( int j=1; j<=n; j++ ){
                if( p[j-1]!='*' )
                    dp[i][j] = dp[i-1][j-1] && ( s[i-1]==p[j-1] || p[j-1]=='.' );
                else
                    dp[i][j] = dp[i][j-2] || ( ( dp[i-1][j-2] || dp[i-1][j] ) && (s[i-1]==p[j-2] || p[j-2]=='.'));
            }
        }
        return dp[m][n];
    }
};